Bugs Integrated, Inc.
Bugs Integrated, Inc. is a major manufacturer of advanced memory chips. They
are launching production of a new six terabyte Q-RAM chip. Each chip consists of
six unit squares arranged in a form of a 2×3 rectangle. The way Q-RAM chips are
made is such that one takes a rectangular plate of silicon divided into N×M unit
squares. Then all squares are tested carefully and the bad ones are marked with
a black marker.
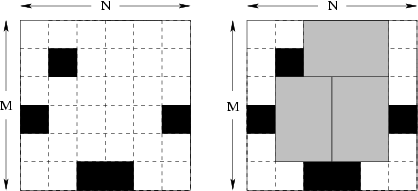
Finally, the plate of silicon is cut into memory chips. Each chip consists of
2×3 (or 3×2) unit squares. Of course, no chip can contain any bad (marked)
squares. It might not be possible to cut the plate so that every good unit
square is a part of some memory chip. The corporation wants to waste as little
good squares as possible. Therefore they would like to know how to cut the plate
to make the maximum number of chips possible.
Task
You are given the dimensions of several silicon plates and a list of all bad
unit squares for each plate. Your task is to write a program that computes for
each plate the maximum number of chips that can be cut out of the plate.
Input description
The first line of the input file consists of a single integer D
(1<=D<=5), denoting the number of silicon plates. D blocks follow, each
describing one silicon plate. The first line of each block contains three
integers N (1<=N<=150), M (1<=M<=10), K (0<=K<=MN) separated
by single spaces. N is the length of the plate, M is its height and K is the
number of bad squares in the plate. The following K lines contain a list of bad
squares. Each line consists of two integers x and y (1<=x<=N,
1<=y<=M) - coordinates of one bad square (the upper left square has
coordinates ).
Output description
For each plate in the input file output a single line containing the maximum
number of memory chips that can be cut out of the plate.
Example input
2
6 6 5
1 4
4 6
2 2
3 6
6 4
6 5 4
3 3
6 1
6 2
6 4
Example output
3
4
Conqueror's battalion
In the whole history of mankind one can find several curious battles, like
the following one in France, in 1747...
There was a fortress in Bassignac-le-Haut, a small village lying on the left
bank of river Dordogne, just over the Chastang dam. From the dam up to the
fortress there was a wide staircase made out of "#008DDC" marble. One day in the
morning, the guard spotted a large battalion approaching the fortress, with a
dreaded leader - The Conqueror.
When The Conqueror reached the fortress, he was already awaited by its
commandant. As the commandant had only a small part of his soldiery available,
he proposed to The Conqueror: "I see that you have many soldiers behind you,
standing on the stairs. We can play a small 'game': In each round, you will
divide your soldiers into two groups in an arbitrary way. Then I will decide
which one of them stays and which one goes home. Each soldier that stays will
then move up one stair. If at least one of your soldiers reaches the uppermost
stair, you will be the winner, in the other case, you will be the loser. And
your destination will be the dam down there...", added the commandant,
pointing to the Chastang dam by his hand.
The Conqueror immediately liked this game, so he agreed and started to
'conquer'.
Task
Your role is The Conqueror's now. There are N stairs to the fortress
(2<=N<=2000) and you have at most 1 000 000 000 soldiers. For each stair,
you are given the number of soldiers standing on it, with number 1 being the
uppermost stair and N the bottom one. None of your soldiers stands on stair 1 at
the beginning.
For each starting position given to your program, if the position is winning
(i.e. there is a strategy that enables you to win the game regardless of your
opponent's moves), your program should win. Otherwise it should just play the
game (and lose) correctly.
This is an interactive problem; you will play against a library as specified
below. In each round, your program will describe a group of soldiers to our
library. The library returns 1 or 2 specifying which group of
soldiers should stay (1 means the group you described, 2 means
the rest of the soldiers). In case the game ends (either because you won or
there are no more soldiers in the game), the library will terminate your program
correctly. Your program may not terminate in any other way.
Library interface
The library libconq provides two routines:
- start - returns the number N and fills an array stairs
with numbers of soldiers standing on the stairs (i.e. there are
stairs soldiers standing on stair i)
- step - takes an array subset (with at least N elements),
describing the group of soldiers you chose, and returns 1 or 2 as described
above; the group of soldiers is specified by numbers of soldiers on each
stair, as in the start function
If you fail to specify a
valid group of soldiers, the game will be terminated and your program will score
zero points for the particular test case. Please note that also in C/C++ the
stairs are numbe"#008DDC" starting from 1.
Following are the declarations of these routines in FreePascal and C/C++:
procedure start(var N: longint; var stairs:array of longint);
function step(subset:array of longint): longint;
void start(int *N, int *stairs);
int step(int *subset);
Below you can find examples of library usage in both FreePascal and C/C++;
both fragments do the same - start the game and then play one round, with the
chosen group containing all soldiers on randomly chosen stairs. Your real
program will probably play the rounds in an infinite loop.
You are strongly encouraged to define the arrays stairs and subset in the
same way as they are defined in the example below. (Note that the FreePascal
library returns its answer in the first N elements of the array regardless of
how you defined it, the C/C++ library returns its answer in the elements with
indices 1 to N.)
FreePascal example
uses libconq;
var stairs: array of longint;
subset: array of longint;
i,N,result: longint;
...
start(N,stairs);
...
for i:=1 to N do
if random(2)=0 then
subset:=0
else
subset;
result:=step(subset);
...
C/C++ example
#include "libconq.h"
int stairs;
int subset;
int i,N,result;
...
start(&N, stairs);
...
for (i=1;i<=N;i++)
if (rand()%2==0)
subset=0;
else
subset;
result=step(subset);
...
You have to link the library to your program - by uses libconq; in
FreePascal and by #include "libconq.h" in C/C++, where you have to
compile your program by adding libconq.c to the compiler arguments.
An example of the game
On the web page you may find example libraries for both C/C++ and FreePascal.
These libraries are different from those that will be used during testing. You
may use them to make sure your library calls are correct. The example library
reads the input from the file libconq.dat, containing two lines. On the
first line is the number N of stairs, the second line contains N integers - the
numbers of soldiers on each of the stairs 1..N.
A decorative fence
Richard just finished building his new house. Now the only thing the house
misses is a cute little wooden fence. He had no idea how to make a wooden fence,
so he decided to order one. Somehow he got his hands on the ACME1Fence Catalogue
2002, the ultimate resource on cute little wooden fences. After reading its
preface he already knew, what makes a little wooden fence cute.
A wooden fence consists of N wooden planks, placed vertically in a row next
to each other. A fence looks cute if and only if the following conditions are
met:
- The planks have different lengths, namely 1, 2, ..., N plank length units.
- Each plank with two neighbors is either larger than each of its neighbors
or smaller than each of them. (Note that this makes the top of the fence
alternately rise and fall.)
It follows, that we may uniquely describe
each cute fence with N planks as a permutation a1,..., aN
of the numbers 1, ..., N such that (for all i;1<i<N) (ai -
ai-1)*(ai - ai+1)>0 and vice versa, each
such permutation describes a cute fence.
It is obvious, that there are many different cute wooden fences made of N
planks. To bring some order into their catalogue, the sales manager of ACME
decided to order them in the following way: Fence A (represented by the
permutation a1,..., aN) is in the catalogue before fence B
(represented by b1, ..., bN) if and only if there exists
such i, that (for all j<i)(aj=bj) and
ai<bi. (Also to decide, which of the two fences is
earlier in the catalogue, take their corresponding permutations, find the first
place on which they differ and compare the values on this place.) All the cute
fences with N planks are numbe"#008DDC" (starting from 1) in the order they appear in
the catalogue. This number is called their catalogue number.

All cute fences
made of N = 4 planks, orde"#008DDC" by their catalogue numbers.
After carefully examining all the cute little wooden fences, Richard decided
to order some of them. For each of them he noted the number of its planks and
its catalogue number. Later, as he met his friends, he wanted to show them the
fences he orde"#008DDC", but he lost the catalogue somewhere. The only thing he has
got are his notes. Please help him find out, how will his fences look like.
Input description
The first line of the input file contains the number K (1<=K<=100) of
input data sets. K lines follow, each of them describes one input data set.
Each of the following K lines contains two integers N and C (1<=N<=20),
separated by a space. N is the number of planks in the fence, C is the catalogue
number of the fence.
You may assume, that the total number of cute little wooden fences with 20
planks fits into a 64-bit signed integer variable (long long in C/C++,
int64 in FreePascal). You may also assume that the input is correct, in
particular that C is at least 1 and it doesn't exceed the number of cute fences
with N planks.
Output description
For each input data set output one line, describing the C-th fence with N
planks in the catalogue. More precisely, if the fence is described by the
permutation a1, ..., aN, then the corresponding line of
the output file should contain the numbers ai (in the correct order), separated
by single spaces.
Example input
2
2 1
3 3
Example output
1 2
2 3 1
A highway and the seven dwarfs
Once upon a time, there was a land where several families of dwarfs were
living. This land was called Dwarfland. Each family lived in one house. Dwarfs
were often visiting their friends from the other families. Because the Dwarfland
was free of evil, it happened that each dwarf visited each other during some
short period of time.
Once, the humans living in countries around Dwarfland decided to build
several straight highways. As the humans weren't aware of the dwarfs, some of
the planned highways passed through Dwarfland. The dwarfs discove"#008DDC" this and
were quite unhappy about it. The dwarfs are very little, and also very slow, so
they are unable to cross the highway safely.
The dwarfs managed to get the plans for the highways somehow, and now they
need your help. They would like to keep on visiting each other, so they don't
like those highways which divide their houses into two non-empty parts. After
they find out which highways they don't like, they will magically prevent the
humans from building them.
The dwarfs are very little, and cannot reach the keyboard. So they asked for
your help.
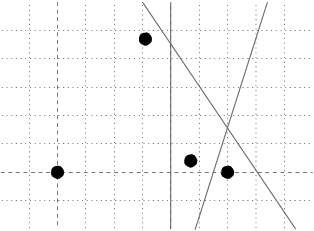
Task
Given is a number N of points (houses) in the plane and several straight
lines (highways). For each given line, your task is to determine whether all N
points lie on the same side of the line or not. Your program has to output the
answer for the currently processed line before reading the description of
the next one. You may assume that no highway passes through any of the houses.
Input and output description
Your program is supposed to read the input from the standard input
(stdin in C/C++, input in FreePascal) and write its output to
the standard output (stdout in C/C++, output in FreePascal).
The first line of the input contains one integer N (0<=N<=100 000). N
lines follow, the i-th of them contains two real numbers xi,
yi (-109<=xi,
yi<=109) separated by a single space - the coordinates
of the i-th house.
Each of the following lines contains four real numbers X1,
Y1, X2, Y2 (-109<=X1,
Y1, X2, Y2<=109) separated by a
single space. These numbers are the coordinates of two different points
, lying on the
highway. For each line of input, your program is supposed to output a line
containing the string "GOOD" if all of the given points are on the same
side of the given line, or "BAD" if the given line divides the points.
After writing out each line of the output, your program should flush the output
buffer. In the following sections you may find an example on how to do this.
We will terminate your program after it gives the answer for the last
highway. Your program is not supposed to terminate by itself. You may
assume that there will be no more than 100 000 highways.
Input and output routines in C/C++
Reading one line (note that there is no space after the last %lf):
double X_1, Y_1, X_2, Y_2;
scanf(" %lf %lf %lf %lf",&X_1,&Y_1,&X_2,&Y_2);
Writing the output for one line: printf("GOOD\n"); fflush(stdout);
Input and output routines in FreePascal
Reading one line:
var X_1, Y_1, X_2, Y_2 : double;
read(X_1,Y_1,X_2,Y_2);
Writing the output for one line: writeln('GOOD'); flush(output);
Warning
You are adviced to use the double data type (in both C/C++ and
FreePascal) to store real numbers. Note that when using real number arithmetics,
rounding errors may occur. If you want to test, whether two real numbers x, y
are equal, don't test whether x = y but whether |x-y|<e (where e is a small
constant, 10-4 will suffice).
Example input
4
0.0 0
6.00 -0.001
3.125 4.747
4.747 0.47
5 3 7 0
4 -4.7 7 4.7
4 47 4 94
Example output
GOOD
BAD
BAD
Royal guards
Once upon a time, there was a kingdom. It had everything a kingdom needs,
namely a king and his castle. The ground-plan of the castle was a rectangle that
was divided into M×N unit squares. Some of the squares are walls, some of them
are free. We will call each of the free squares a room. The king of our
kingdom was extremely paranoid, so one day he decided to make hidden pits (with
alligators at the bottom) in some of the rooms.
But this was still not enough. One week later, he decided to place as many
guards as possible inside his castle. However, this won't be so simple. The
guards are trained so that immediately after they see someone, they shoot at
him. And so the king has to place the guards carefully, because if two guards
would see each other, they would shoot at themselves! Also evidently the king
can't place a guard into a room with a pit.
Two guards in a room see each other, so each room may contain at most one
guard. Two guards in different rooms see each other if and only if the squares
corresponding to their rooms are in the same row or in the same column of the
plan of the castle and there is no wall between them. (The guard can see
only in four directions, much like a rook in chess.)
Task
Your task is to find out, how many guards can the king place inside his
castle (according to the rules above) and to find one possible assignment of
that many guards into the rooms.
Input description
The first line of the input file contains two numbers M, N, 1<=M,N<=200
- the dimensions of the ground-plan of the castle. The i-th of the following M
lines contains N numbers ai,1, ..., ai,N, separated by
single spaces, where:
- ai,j=0 means that the square is free (a room without a
pit)
- ai,j=1 means that the square contains a pit
- ai,j=2 means that the square is a wall
Note that
the first coordinate of a square is the row and the second one is the column.
Output description
The first line of the output file should contain the maximum number K of
guards the king may place inside his castle. The following K lines should
contain one possible assignment of K guards into the free rooms of the castle so
that no two guards would see each other.
More precisely, the i-th of these lines should contain two integers
ri, ci separated by a single space - the coordinates of
the room where i-th guard will be placed (ri is the row and
ci is the column).
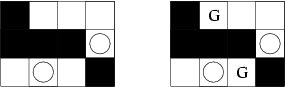
Castle from the
example input and one possible correct output
Example input
3 4
2 0 0 0
2 2 2 1
0 1 0 2
Example output
2
1 2
3 3
Birthday party
John's birthday is approaching slowly, and as every year, John is going to
organize a great garden party. He wants all his friends to come, but (sadly) he
knows, that it is almost impossible. For example Susie left Steve last week, and
it will be almost impossible to make both of them come. John spent most of the
last week visiting his friends and asking them to come. He got some promises,
but even more requests. ('If you invite me, you just have to invite my
boyfriend!' exclaimed Veronica. 'If you invite the Burdiliak twins, don't expect
me or Joseph to come!' stated Peter.) Suddenly, John realized, that it will be
quite hard just to satisfy all the requests he got.
Task
You are given a description of the requests John got from his friends. Your
task is to find a group of people such that if John invites the people in this
group (and nobody else) to his party, all the requests he got will be satisfied.
The requests are described in the following way:
- name is a request. This request is satisfied if and only if John
invites name.
- -name is a request. This request is satisfied if and only if John
doesn't invite name. (In both cases, name is a string of at
most 20 lowercase letters without spaces.)
- If R1, ..., Rk are requests, then (R1 & ...
& Rk) is a request. This request is satisfied if and only if all
requests R1, ..., Rk are satisfied.
- If R1, ..., Rk are requests, then (R1 | ... |
Rk) is a request. This request is satisfied if and only if at least one
of the requests R1, ..., Rk is satisfied.
- If R1, R2 are requests, then (R1=>R2) is a
request. This request is not satisfied if and only if R1 is
satisfied and R2 is not satisfied.
Input description
You can find ten input files, called party1.in to
party10.in, here.
On the first line of the input file is the number of John's friends F, next F
lines contain their names, one per line. On the next line is the number of
requests N. Each of the following N lines contains one request.
Output description
For each file partyX.in you have to produce the corresponding output
file partyX.out, containing one correct solution. The first line of the
output file will be the number K of people John should invite. The following K
lines should contain their names, one per line. You may assume that each of the
input files has a (not necessarily unique) solution. If there are more possible
solutions, you may output any of them.
Example input
3
veronica
steve
dick
3
(veronica => dick)
(steve => -veronica)
(steve & dick)
Example output
2
steve
dick