Zadanie: Akcja komandosów

Na Pustyni Błędowskiej odbywa się w tym roku Bardzo Interesująca i Widowiskowa Akcja Komandosów (BIWAK). Podstawowym elementem BIWAK-u ma być neutralizacja bomby, która znajduje się gdzieś na pustyni, jednak nie wiadomo dokładnie gdzie.

Pierwsza część akcji to desant z powietrza. Z helikoptera krążącego nad pustynią, wyskakują pojedynczo, w ustalonej kolejności komandosi. Gdy któryś z komandosów wyląduje w jakimś miejscu, okopuje się i już się z nie rusza z miejsca. Dopiero potem może wyskoczyć kolejny komandos.

Dla każdego komandosa określona jest pewna odległość rażenia. Jeśli komandos przebywa w tej odległości (lub mniejszej) od bomby, to w przypadku jej ewentualnej eksplozji zginie. Dowództwo chce zminimalizować liczbę komandosów biorących udział w akcji, ale chce mieć pewność, że w przypadku wybuchu bomby, przynajmniej jeden z komandosów przeżyje.

Na potrzeby zadania przyjmujemy, że Pustynia Błędowska jest płaszczyzną, a komandosów, którzy się okopali utożsamiamy z punktami. Mamy dany ciąg kolejno mogących wyskoczyć komandosów. Żaden z nich nie może opuścić swojej kolejki, tzn. jeśli i-ty komandos wyskakuje z samolotu, to wszyscy poprzedni wyskoczyli już wcześniej. Dla każdego z komandosów znamy jego odległość rażenia oraz współrzędne punktu, w którym wyląduje, o ile w ogóle wyskoczy.

Zadanie

Napisz program, który:

wczyta ze standardowego wejścia opisy komandosów,
wyznaczy minimalną ilość komandosów, którzy muszą wyskoczyć,
wypisze wynik na standardowe wyjście.

Wejście

W pierwszym wierszu standardowego wejścia zapisana jest jedna liczba całkowita n ( 2 <= n <= 2 000) -- liczba komandosów. W kolejnych n wierszach opisani są komandosi -- po jednym w wierszu. Opis każdego komandosa składa się z trzech liczb całkowitych: x, y i r ( -1000 <= x, y <= 1000, 1 <= r <= 5000). Punkt (x, y) to miejsce, gdzie wyląduje komandos, a r to jego odległość rażenia. Jeśli komandos znajdzie się w odległości r lub mniejszej od bomby, to w przypadku jej wybuchu zginie.

Wyjście

W pierwszym i jedynym wierszu standardowego wyjścia Twój program powinien zapisać jedną liczbę całkowitą -- minimalną liczbę komandosów, którzy muszą wyskoczyć, aby zapewnić, że co najmniej jeden z nich przeżyje, lub jedno słowo NIE jeśli nie jest możliwe, aby mieć pewność, że któryś z komandosów przeżyje.

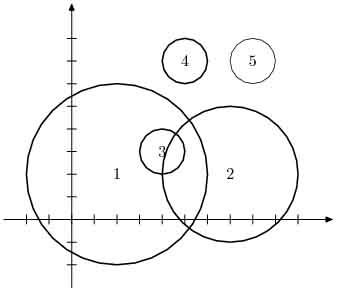
Przykład

Dla danych wejściowych:

poprawną odpowiedzią jest:

Uwaga

To zadanie można rozwiązać używając typów zmiennopozycyjnych:

w Pascalu: double lub extended,
w C oraz C++: double lub long double.

Użycie typów float lub real może spowodować błędy w obliczeniach związane z niedokładnością operacji zmiennopozycyjnych.

Wersja do druku