

| XVIII OI 2010/2011 |  |

Zadanie: Autobus
Ulice Bajtogrodu tworzą szachownicę -- prowadzą z północy na południe, lub ze wschodu na zachód. Ponadto każda ulica prowadzi na przestrzał przez całe miasto -- każda ulica biegnąca z północy na południe krzyżuje się z każdą ulicą biegnącą ze wschodu na zachód i vice versa. Ulice prowadzące z północy na południe są ponumerowane od 1 do n, w kolejności z zachodu na wschód. Ulice prowadzące ze wschód na zachód są ponumerowane od 1 do m, w kolejności z południa na północ. Każde skrzyżowanie i-tej ulicy biegnącej z północy na południe i j-tej ulicy biegnącej ze wschodu na zachód oznaczamy parą liczb (i, j) (dla 1 <= i <= n, 1 <= j <= m).
Po ulicach Bajtogrodu kursuje autobus. Zaczyna on trasę przy skrzyżowaniu (1, 1), a kończy przy skrzyżowaniu (n, m). Ponadto autobus może jechać ulicami tylko w kierunku wschodnim i/lub północnym.
Przy pewnych skrzyżowaniach oczekują na autobus pasażerowie. Kierowca autobusu chce tak wybrać trasę przejazdu autobusu, aby zabrać jak najwięcej pasażerów. (Zakładamy, że bez względu na wybór trasy i tak wszyscy pasażerowie zmieszczą się w autobusie.)
Zadanie
Napisz program, który:- wczyta ze standardowego wejścia opis siatki ulic oraz liczbę pasażerów czekających przy poszczególnych skrzyżowaniach,
- obliczy ilu maksymalnie pasażerów może zabrać autobus,
- wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu pliku wejściowego zapisane są trzy dodatnie liczby całkowite n, m i k -- odpowiednio: liczba ulic biegnących z północy na południe, liczba ulic biegnących ze wschodu na zachód i liczba skrzyżowań, przy których pasażerowie czekają na autobus ( 1 <= n <= 109, 1 <= m <= 109, 1 <= k <= 105).Kolejne k wierszy opisuje rozmieszczenie pasażerów czekających na autobus, w jednym wierszu opisani są pasażerowie czekający na jednym ze skrzyżowań. W wierszu i + 1 znajdują się trzy dodatnie liczby całkowite xi, yi i pi, oddzielone pojedynczymi odstępami, 1 <= xi <= n, 1 <= yi <= m, 1 <= pi <= 106. Taka trójka liczb oznacza, że przy skrzyżowaniu (xi, yi) oczekuje pi pasażerów. Każde skrzyżowanie pojawia się w danych wejściowych co najwyżej raz. Łączna liczba oczekujących pasażerów nie przekracza 1 000 000 000.
Wyjście
Twój program powinien na wyjściu wypisać jeden wiersz zawierający jedną liczbę całkowitą -- maksymalną liczbę pasażerów, których może zabrać autobus.
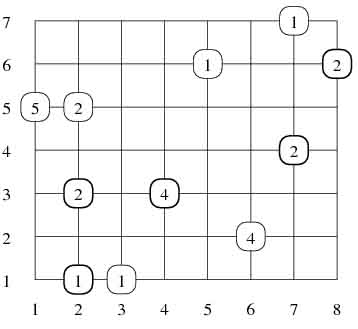
Przykład
Dla danych wejściowych:8 7 11 4 3 4 6 2 4 2 3 2 5 6 1 2 5 2 1 5 5 2 1 1 3 1 1 7 7 1 7 4 2 8 6 2poprawną odpowiedzią jest:
11