Drzewo binarne może byc puste, albo składać sie z wierzchołka, do którego przyczepione są dwa drzewa, tzw. lewe i prawe poddrzewo. W każdym wierzchołku zapisana jest jedna litera alfabetu angielskiego. Wierzchołek drzewa, który nie znajduje się w żadnym poddrzewie, nazywamy korzeniem. Mówimy, że drzewo jest binarnym drzewem poszukiwań (BST), jeżeli dla każdego wierzchołka spełniony jest warunek, mówiący, że wszystkie litery z lewego poddrzewa wierzchołka występują w alfabecie wcześniej, niż litera zapisana w wierzchołku, natomiast wszystkie litery z prawego poddrzewa - później. Kodem drzewa BST nazywamy:
Istnieje dokładnie 14 kodów 4-wierzchołkowych binarnych drzew poszukiwań, konkretnie (w kolejności alfabetycznej):
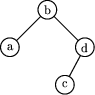
Napis badc jest (7,4)-kodem i odpowiada mu następujące drzewo BST:

Napisz program, który:
W pierwszym i jedynym wierszu pliku tekstowego KOD.IN zapisane są dokładnie dwie dodatnie liczby całkowite n i k, oddzielone pojedynczym znakiem odstępu, 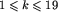 . Liczba n nie przekracza liczby kodów drzew BST o k wierzchołkach.
. Liczba n nie przekracza liczby kodów drzew BST o k wierzchołkach.
W pierwszym i jedynym wierszu pliku tekstowego KOD.OUT powinno znajdować się słowo złożone z małych liter alfabetu angielskiego będące (n,k)-kodem.
11 4poprawną odpowiedzią jest plik wyjściowy KOD.OUT
dacb
Zastanówmy się najpierw, ile jest drzew binarnych o zadanej liczbie wierzchołków. Oznaczmy przez Ck liczbę drzew mających k wierzchołków. Oczywiście C_0=1: tylko drzewo puste ma zero wierzchołków. Również jest tylko jedno drzewo mające jeden wierzchołek, zatem C_1=1. Niech teraz k będzie liczbą naturalną większą od jedności. Drzewo mające k wierzchołków składa się z korzenia, do którego przyczepione są dwa poddrzewa mające łącznie k-1 wierzchołków. Mamy więc k możliwości:
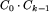 ).
).
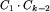 );
);
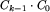 ).
).
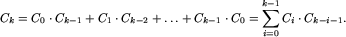
Liczby Ck nazywamy liczbami Catalana. Występują one w wielu innych zadaniach kombinatorycznych. Na przykład:
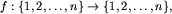
 , to
, to 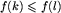 dla dowolnych
dla dowolnych 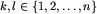 i spełniających warunek
i spełniających warunek 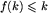 , dla każdego
, dla każdego 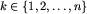 , jest równa Cn.
, jest równa Cn.
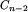 .
.
 i rozważamy wyrażenie postaci
i rozważamy wyrażenie postaci 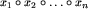 . W tym wyrażeniu możemy rozstawić nawiasy (tak, by zawsze wykonywać działanie na dwóch argumentach) na wiele sposobów. Na przykład, dla n=4 mamy następujące sposoby:
. W tym wyrażeniu możemy rozstawić nawiasy (tak, by zawsze wykonywać działanie na dwóch argumentach) na wiele sposobów. Na przykład, dla n=4 mamy następujące sposoby: 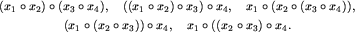
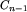 . Inaczej mówiąc, jeśli działanie
. Inaczej mówiąc, jeśli działanie  jest niełączne (przykładem takiego działania jest dzielenie liczb rzeczywistych dodatnich), to wykonując to działanie na wszystkie możliwe sposoby, z zachowaniem kolejności x_1,x_2,...,x_n, możemy otrzymać co najwyżej
jest niełączne (przykładem takiego działania jest dzielenie liczb rzeczywistych dodatnich), to wykonując to działanie na wszystkie możliwe sposoby, z zachowaniem kolejności x_1,x_2,...,x_n, możemy otrzymać co najwyżej 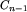 różnych wyników.
różnych wyników.
Podany wyżej wzór rekurencyjny pozwala obliczyć kolejne liczby Catalana. Początkowe liczby Catalana są równe odpowiednio:
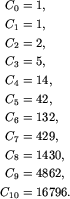
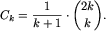
Teraz opiszemy algorytm znajdowania (n,k)-kodu drzewa binarnego. Najpierw wyjaśnimy istotę działania tego algorytmu na przykładzie. Przyjmijmy k=10 i n=8751. Wiemy już, że istnieje 16796 drzew binarnych mających 10 wierzchołków. Ta liczba jest sumą następujących 10 liczb:
1. liczby 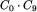 , równej 4862; jest to liczba tych drzew, w których lewe poddrzewo ma 0 wierzchołków, a prawe 9 wierzchołków; są to dokładnie te drzewa binarne, które mają w korzeniu umieszczoną literę a;
, równej 4862; jest to liczba tych drzew, w których lewe poddrzewo ma 0 wierzchołków, a prawe 9 wierzchołków; są to dokładnie te drzewa binarne, które mają w korzeniu umieszczoną literę a;
2. liczby 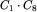 , równej 1430; jest to liczba tych drzew, w których lewe poddrzewo ma 1 wierzchołek, a prawe 8 wierzchołków; są to drzewa, które mają w korzeniu umieszczoną literę b;
, równej 1430; jest to liczba tych drzew, w których lewe poddrzewo ma 1 wierzchołek, a prawe 8 wierzchołków; są to drzewa, które mają w korzeniu umieszczoną literę b;
3. liczby 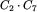 , równej 858; jest to liczba tych drzew, w których lewe poddrzewo ma 2 wierzchołki, a prawe 7 wierzchołków; są to drzewa, które mają w korzeniu umieszczoną literę c;
, równej 858; jest to liczba tych drzew, w których lewe poddrzewo ma 2 wierzchołki, a prawe 7 wierzchołków; są to drzewa, które mają w korzeniu umieszczoną literę c;
...
10. liczby 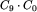 , równej 4862; jest to liczba tych drzew, w których lewe poddrzewo ma 9 wierzchołki, a prawe 0 wierzchołków; są to drzewa, które mają w korzeniu umieszczoną literę j.
, równej 4862; jest to liczba tych drzew, w których lewe poddrzewo ma 9 wierzchołki, a prawe 0 wierzchołków; są to drzewa, które mają w korzeniu umieszczoną literę j.
Kody wszystkich drzew z grupy pierwszej poprzedzają oczywiście w porządku alfabetycznym kody drzew z grupy drugiej, te z kolei poprzedzają kody drzew w grupy trzeciej itd. Zauważmy teraz, że łączna liczba kodów zaczynających się od liter a, b, c, d, e jest równa 8398 (czyli mniej niż 8751), a jeśli dopuścimy jeszcze literę f, to liczba kodów wyniesie 8986 (a więc więcej niż 8751). Stąd wynika, że pierwszą literą kodu jest f. Po niej nastąpią litery od a do e (w nieznanej jeszcze kolejności) i na końcu litery od g do j (również w nieznanej kolejności). W ten sposób ustaliliśmy pierwszą literę kodu drzewa. Następnie będziemy chcieli ustalić kody obu poddrzew. W tym celu obliczymy kolejne numery tych kodów i rekurencyjnie znajdziemy same kody.
Każdemu z C5 kodów złożonych z liter od a do e na początku odpowiada C4 kodów złożonych z liter od g do j na końcu. Mamy znaleźć 353-ci z kolei kod rozpoczynający się literą f (gdyż 8751-8398=353). Każdemu kodowi lewego poddrzewa odpowiada 14 kodów prawych poddrzew. Ale 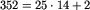 . Stąd wynika, że odcinek początkowy naszego kodu (po literze f) ma być dwudziestym szóstym z kolei kodem składającym się z liter od a do e, a odcinek końcowy ma być trzecim z kolei kodem składającym się z liter od g do j. Jest tak dlatego, że pierwszym dwudziestu pięciu kodom lewych poddrzew odpowiada tylko
. Stąd wynika, że odcinek początkowy naszego kodu (po literze f) ma być dwudziestym szóstym z kolei kodem składającym się z liter od a do e, a odcinek końcowy ma być trzecim z kolei kodem składającym się z liter od g do j. Jest tak dlatego, że pierwszym dwudziestu pięciu kodom lewych poddrzew odpowiada tylko  czyli 350 kodów całych drzew. Nasz kod ma więc być trzecim kodem z następnej, tzn. dwudziestej szóstej grupy. Powstaje pytanie, dlaczego dzielimy 352, a nie 353. Mianowicie mamy proste wzory ogólne na numer grupy (czyli numer kodu lewego poddrzewa) i numer w tej grupie (czyli numer kodu prawego poddrzewa):
czyli 350 kodów całych drzew. Nasz kod ma więc być trzecim kodem z następnej, tzn. dwudziestej szóstej grupy. Powstaje pytanie, dlaczego dzielimy 352, a nie 353. Mianowicie mamy proste wzory ogólne na numer grupy (czyli numer kodu lewego poddrzewa) i numer w tej grupie (czyli numer kodu prawego poddrzewa):
przypuśćmy, że nasz kod ma być m-tym kodem zaczynającym się od pewnej znanej już litery c (w naszym przypadku 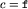 ); znamy więc wielkości obu poddrzew: niech lewe składa się z l wierzchołków, a prawe z p wierzchołków. Wtedy lewe poddrzewo ma numer
); znamy więc wielkości obu poddrzew: niech lewe składa się z l wierzchołków, a prawe z p wierzchołków. Wtedy lewe poddrzewo ma numer 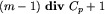 , a prawe
, a prawe 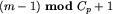 .
.
Kontynuując obliczenia w naszym przykładzie zauważymy, że odcinek początkowy kodu zaczyna się literą d, po której następuje trzeci kod składający się z liter a, b, c i jedyny kod składający się z litery e. Odcinek końcowy zaczyna się literą g, po której następuje trzeci kod składający się z liter h, i, j. Ostatecznie otrzymamy kod fdbacegihj.
Teraz już nietrudno napisać odpowiedni algorytm rekurencyjny. Główna funkcja wyznaczająca (n,k)-kod ma w nim postać następującą. Argumentami funkcji są: litera cp, od której zaczynają się litery umieszczone w wierzchołkach drzewa (będzie to potrzebne w przypadku prawego poddrzewa, w którym występują litery nie od początku alfabetu), numer n drzewa i liczba wierzchołków k. W tablicy Catalan umieszczone są oczywiście liczby Catalana, obliczone wcześniej za pomocą wzoru rekurencyjnego. Na początku funkcja zwraca wartości w przypadkach najprostszych: kod pusty dla drzewa pustego i kod jednoliterowy cp dla drzewa składającego się z jednego wierzchołka. Dla drzew większych obliczamy w pętli sumę iloczynów liczb Catalana dotąd, aż przekroczy ona n. Zauważmy, że wartości zmiennych l i p są wtedy równe dokładnie liczbom wierzchołków w lewym i prawym poddrzewie. Korzeń otrzymujemy znajdując literę stojącą w alfabecie o l miejsc dalej od cp. Potem zgodnie z powyższymi wzorami znajdujemy numery lewego i prawego poddrzewa i dwukrotnie wywołujemy procedurę rekurencyjnie. Otrzymane kody drzew łączymy wreszcie ze znalezionym wcześniej korzeniem. Oto treść tej procedury:
| 1 | function Kod (cp : char; n : longint; k : integer) : String; |
| 2 | { cp : litera początkowa kodu drzewa; |
| 3 | n : numer kodu drzewa wśród drzew mających wierzchołki |
| 4 | oznaczone literami począwszy od cp zakładamy, że liczba |
| 5 | n nie przekracza liczby Catalana C[k]; |
| 6 | k : liczba wierzchołków drzewa} |
| 7 | var |
| 8 | l,p : integer; {liczba wierzchołków w lewym i prawym poddrzewie} |
| 9 | Suma : longint; {suma iloczynów liczb Catalana} |
| 10 | SumaPoprzednia : longint; |
| 11 | m : longint; |
| 12 | n1,n2 : longint; {numery lewego i prawego poddrzewa} |
| 13 | znak : char; |
| 14 | begin |
| 15 | if (k=0) then |
| 16 | Kod:=`' |
| 17 | end if (k=1) then |
| 18 | Kod:=cp |
| 19 | end begin |
| 20 | Suma:=0; |
| 21 | l:=-1; |
| 22 | p:=k; |
| 23 | repeat |
| 24 | l:=l+1; |
| 25 | p:=p-1; |
| 26 | SumaPoprzednia:=Suma; |
| 27 | Suma:=Suma+Catalan[l]*Catalan[p]; |
| 28 | until (Suma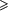 n); n); |
| 29 | znak:=chr(ord(cp)+l); |
| 30 | m:=n-SumaPoprzednia; |
| 31 | n1:=((m-1) div Catalan[p])+1; |
| 32 | n2:=((m-1) mod Catalan[p])+1; |
| 33 | Kod:=znak+Kod(cp,n1,l)+Kod(succ(znak),n2,p) |
| 34 | end |
| 35 | end; |
Ten najprostszy program zamieszczony jest w pliku o nazwie kod0.pas. Nie jest on jednak optymalny. Można zauważyć, że pewne obliczenia są wykonywane wielokrotnie, na przykład sumowanie iloczynów liczb Catalana. Te iloczyny i ich sumy można obliczyć wcześniej i umieścić w tablicy. Tak napisany program znajduje się w pliku kod.pas.
Ograniczenie k=19 wynika z wielkości liczb Catalana. Liczba 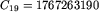 mieści się jeszcze w zakresie liczb typu longint.
mieści się jeszcze w zakresie liczb typu longint.
Do sprawdzania rozwiązań zawodników użyto 17 testów: