| I stage competition |
| Source file: | pun.xxx (xxx=pas,c,cpp) |
| Memory limit: | 32 MB |
Alternative formats: PostScript | PDF
A set of integer points on a plane (points whose both cartesian coordinates are integers) which we shall refer to as the pattern, as well as a group of other sets of integer points on the plane are given. We would like to know which of the sets are similar to the pattern, i.e. which of them can be transformed by rotations, translations, reflections and dilations so that they are identical to the pattern. For instance: the set of points {(0,0), (2,0), (2,1)} is similar to the set {(6,1), (6,5), (4,5)}, it is however not similar to the set {(4,0),(6,0), (5,-1)}.
Write a programme which:
In the first line of the standard input there is a single integer k (1 <= k <= 25.000) - the number of points the pattern consists of. In the following k lines there are pairs of integers, separated by single spaces. The i+1st line containts the coordinates of ith point belonging to the pattern: x_i i y_i (-20.000 <= x_i, y_i <= 20.000). The points forming the pattern are pairwise different. In the next line there is the number of sets to be investigated: n (1 <= n <= 20). Next, there are n descriptions of these sets. The description of each set begins with a line containing a single integer l - the number of points belonging to that particular set (1 <= l <= 25.000). These points are described in the following lines, a single point per line. The description of a point consists of two integers separated by a single space - its coordinates x i y (-20.000 <= x, y <= 20.000). The points which belong to the same set are pairwise different.
Your programme should write to the standard output n lines - one for each of the investigated sets of points. The ith line should contain the word TAK (YES in Polish), if the ith of the given sets of points is similar to the pattern, or the word NIE (NO in Polish) if the set does not satisfy this condition.
For the input data:
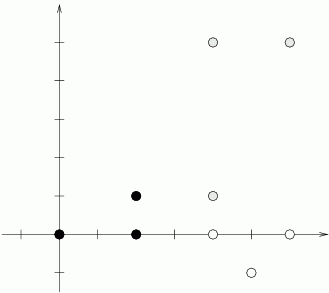
3 0 0 2 0 2 1 2 3 4 1 6 5 4 5 3 4 0 6 0 5 -1
the correct outcome is:
TAK NIE