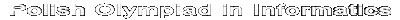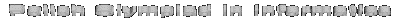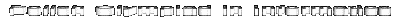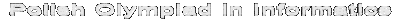


 |

| News |
| About Olympic |
| History of OI |
| OI books |
| National team |
| Olympic camps |
| Photo gallery |
| Links |
| SIO |
| MAIN |
|
X Olympiad in Informatics 2002/2003
|
|
Problem: Connections
|
Author: Krzysztof Sikora
|
Byteotian Ministry of Infrastructure has decided to create a computer program that helps to find quickly the lengths of routes between arbitrary towns. It would be small wonder if the inhabitants of Byteotia always wanted to find the shortest route. However, it happens that they want to know the k-th shortest route. Moreover, cycles in routes are possible, i.e. routes that have recurring towns.
Example
If there are 4 routes between two towns and their lengths are 2, 4, 4 and 5, then the length of the shortest connection is 2, the second shortest is 4, the third is 4, and the fourth is 5.Task
Write a program which:- reads from the standard input a description of Byteotian road network and queries concerning lengths of journey routes,
- computes and writes to the standard output answers to the queries read.
Input
In the first line of the standard input there are two positive integers n and m, separated by a single space, 1 <= n <= 100, 0 <= m <= n2-n. They are the number of towns in Byteotia and the number of roads connecting the towns, respectively. The towns are numbered from 1 to n.
In each of m successive lines there are three integers separated by single spaces: a, b and l, a <> b, 1 <= l <= 500. Each triple describes one one-way road of length l enabling to move from the town a to b. For each two towns there exist at most one road that enables to move in the given direction.
In the following line there is one integer q, 1 <= q <= 10000, denoting the number of queries. In the successive q lines there are queries written, one per line. Each query has a form of three integers separated by single spaces: c, d and k, 1 <= k <= 100. Such a query refers to the length of the k-th shortest route from the town c to the town d.
Output
Your program should write to the standard output the answers to the queries read, one answer per line. In the i-th line the answer to the i-th query should be written: one integer equal to the length of the route being sought or -1, when such a route does not exist.Example
For the following input data:5 5 1 2 3 2 3 2 3 2 1 1 3 10 1 4 1 8 1 3 1 1 3 2 1 3 3 1 4 2 2 5 1 2 2 1 2 2 2 1 1 2the correct answer is in the following output:
5 8 10 -1 -1 3 6 -1

Print friendly version