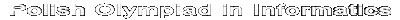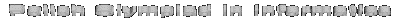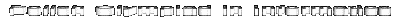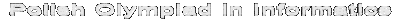


| History of OI |  |

Task: Hollows
There are two extremely high trees in Byteotia, and each of them has many hollows scooped out in its trunk, one under another. Once upon a time n very fast birds decided to inhabit the hollows. Some of them know each other and therefore would like to be able to pay one another visits in their hollows. The birds fly very fast and always along a straight line. In order to avoid the danger of collision they decided to quarter in a way that:
- each two birds that would like to pay themselves visits live in different trees, and
- for each two pairs of familiar birds, the segments connecting the hollows of the familiar birds do not intersect (they may, however, have a common endpoint).
It is well-known that birds have very small brains. That's why they have asked you -- a respected ornithologist -- to help them find out in how many ways they can quarter in the hollows.
Task
Write a programme that:- reads from the standard input the description of acquaintanceship between the birds,
- calculates in how many ways can the birds be quartered in the trees, satisfying the above constraints,
- writes the result to the standard output.
Input
In the first line of the standard input there are three integers written n, m and k, denoting respectively: the number of birds, the number of distinct pairs of birds knowing each other and the number that is to be used when giving result (see: Output), 2 <= n <= 1 000 000, 1 <= m <= 10 000 000, 2 <= k <= 2 000 000. The birds are numbered from 1 to n. In the following m lines the pairs of birds knowing each other are given, one per line. In the line no. i + 1 two integers ai and bi, separated by a single space, are written (1 <= ai, bi <= n, ai <> bi). These are the numbers of the familiar birds. Each (unordered) pair of familiar birds is given exactly once.
Output
Let r denote the number of distinct quarterings of birds satysfying the given constraints. Your programme should write one integer in the first line of the standard output: the remainder of division of r by k. If no quartering exists the correst result is 0.
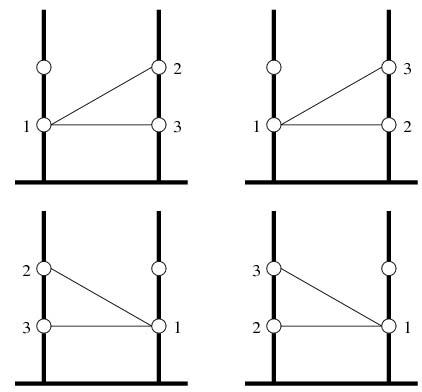
Example
For the following input data:3 2 10 1 2 1 3the correct answer is:
4

Print friendly version