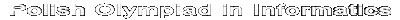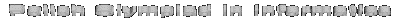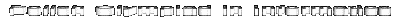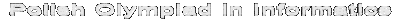


| History of OI |  |

Task: sko
| I stage competition |
| Source file: | sko.xxx (xxx=pas,c,cpp) |
| Memory limit: | 32 MB |
A knight moves on an infinite chessboard. Each move it can perform is described by a pair of integers - a pair (a,b) indicates that a move from the square (with coordinates) (x,y) to the square (x+a,y+b) or (x-a,y-b) is possible. Each knight has a prescribed set of such pairs, describing the moves this knight can make. For each knight we assume that not all squares this knight can move to from square (0,0) are collinear.
We say two knights are equivalent, if they can reach exactly the same squares starting from the square (0,0) (by making many moves, perhaps). (Let us point out that equivalent knights may reach these squares in different number of moves). It can be shown that for every knight there exists an equivalent one whose moves are described by only two pairs of numbers.
Task
Write a programme that:
- reads from the standard input the pairs denoting the knight's moves,
- determines two pairs of integers denoting the moves of an equivalent knight,
- writes these two pairs of integers to the standard output.
Input
In the first line of the standard input one integer n is written, dentoting the number of pairs describing the knight's moves, 3 <= n <= 100. In the following n lines pairs of integers representing the knight's moves are written, one pair per line. In each of these lines two integers a_i and b_i separated by a single space are written, -100 <= a_i, b_i <= 100. We assume that (a_i,b_i) <> (0,0).
Output
In the first line of the standard output two integers a and b separated by a single space should be written, $-10.000 <= a, b <= 10.000. In the second line two integers c and d separated by a single space should be written, -10.000 <= c, d <= 10.000. The above integers should satisfy the condition that a knight whose moves are described by pairs (a,b) and (c,d) is equivalent to the knight described in the input data.
Example
For the following input data:
3 24 28 15 50 12 21
the correct answer is:
468 1561 2805 9356or:
3 0 0 1

Print friendly version