

| History of OI -> II OI 1994/1995 -> Problems |  |

|
II Olympiad in Informatics 1994/1995
|
|
Task: WIE
|
Author: Krzysztof Diks
|
| II stage contest |
We are given a convex polygon P of n sides (where 3 < n <= 5000) and k its distinct diagonals not crossing one another inside the polygon. (The only point that two distinct diagonals may share is a vertex of the polygon.) Vertices of the polygon are numbered successively from 1 to n counterclockwise. All the diagonals divide P into smaller convex polygons whose interiors do not intersect.
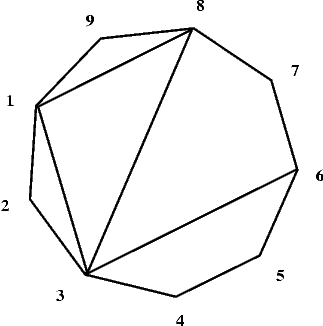
Example
Four diagonals: 1-8, 8-3, 3-1 and 3-6 divide the polygon P shown in the picture below into two quadrilaterals and three triangles.
Task
Write a program that:- reads a description of the polygon P and its diagonals from the text file WIE.IN,
- calculates the maximal number of sides of a polygon among the polygons created by the division of P by the given diagonals,
- writes the result in the text file WIE.OUT.
Input
In each line of the text file WIE.IN two positive integers separated by a single space are written.In the first line there is the number of vertices n of the polygon and the number of diagonals k.
In each of the following k lines there is a description of one diagonal of the polygon in the form of a pair of positive integers. These integers are the numbers of the vertices of the polygon the diagonal joins. Just after the second number there is the end of the line.
The data in the file WIE.IN are written correctly and your program need not verify that.
Output
In the file WIE.OUT one should write one positive integer - the maximal number of sides of a convex polygon created by the division of the given polygon P,Example
For the following file WIE.OUT, which is the description of the polygon and its diagonals presented in the picture:9 4 1 8 8 3 3 1 3 6there should be one number written in the file WIE.OUT:
4
Your program should look for the file WIE.IN in the current directory and create the file WIE.OUT also in the current directory. The source file containing the program written by you should be named WIE.???, where ??? are substituted by at most three-letter abbreviation of the programming language used. The same program in an executable form should be written in a file WIE.EXE.

