

| XVIII OI 2010/2011 |  |

|
XI Olimpiada Informatyczna 2003/2004
|
| Zawody III stopnia |
| Plik źródłowy: | wsc.* |
| Limit pamięci: | 32 MB |
Umowy międzynarodowe podpisane przez Wielce Rozległe Państwo
nakładają na nie obowiązek tranzytowy - musi ono umożliwić
przewiezienie koleją odpadów nuklearnych z elektrowni u
wschodniego sąsiada do punktów utylizacji za zachodnią
granicą.
Względy ekologiczne nakazują taką organizację ruchu,
by pociągi z odpadami jak najszybciej opuściły terytorium kraju.
Sieć kolejowa w tym państwie ma bardzo szczególną strukturę.
Składa się ona z n miast-węzłów kolejowych oraz n-1 dwukierunkowych
odcinków torów, łączących miasta-węzły.
Między każdymi dwoma miastami istnieje możliwość przejazdu.
Ponadto istnieje
taki odcinek sieci, którego końce nie są miastami granicznymi,
oraz każdy przejazd z miasta na granicy wschodniej do miasta na
granicy zachodniej prowadzi przez ten odcinek.
Wszystkie pociągi z odpadami przyjeżdżają na granicę wschodnią
tego samego dnia
przed świtem, przy czym każdy z nich do innego miasta.
Ze względu na niebezpieczeństwo wypadku
pociągi jeżdżą tylko w dzień i po żadnym odcinku nie może
jednocześnie jechać więcej niż jeden pociąg z odpadami,
natomiast dowolnie
wiele takich pociągów może oczekiwać w mieście-węźle.
Dodatkowo przejechanie jednego odcinka zajmuje pociągowi jeden dzień.
Ruch
musi być tak zorganizowany, by każdy pociąg z odpadami
dojechał do innego przejścia na granicy zachodniej.
Ile co najmniej dni pociągi z odpadami muszą spędzić na
terytorium Wielce Rozległego Państwa?
Zadanie
Zadanie polega na napisaniu programu, który:
- wczyta ze standardowego wejścia opis sieci kolejowej i przejść granicznych, do których przyjechały pociągi z odpadami;
- wyznaczy minimalną liczbę dni, jakie musi trwać tranzyt;
- wypisze znalezioną liczbę na standardowe wyjście.
Wejście
Pierwsza linia wejścia zawiera trzy pooddzielane
pojedyńczymi odstępami liczby naturalne
1 < n, w, z < 106, n >= w+z+2.
Liczba n oznacza liczbę miast-węzłów (są one
ponumerowane od 1 do n), zaś w i z oznaczają liczby
przejść granicznych odpowiednio na granicy wschodniej i
zachodniej. Przejścia na granicy wschodniej oznaczone są
liczbami 1,..., w, zaś na zachodniej liczbami
n-z+1,...,n.
W kolejnych n-1 liniach znajduje się opis odcinków sieci
kolejowej. Każda linia opisu zawiera dwie różne liczby naturalne
oddzielone pojedynczym odstępem, 1 < a,b < n.
Są to numery
miast-węzłów połączonych odcinkiem torów.
W n+1-ej linii znajduje się jedna liczba naturalna p, 1 <
p < w, 1 < p < z oznaczająca liczbę pociągów z
odpadami.
W następnej (i ostatniej) linii wejścia znajduje się p
pooddzielanych pojedyńczymi odstępami różnych liczb naturalnych,
z których
każda jest nie większa niż w. Są to numery przejść
granicznych na granicy wschodniej,
do których przyjechały pociągi z odpadami.
Wyjście
Pierwsza i jedyna linia wyjścia powinna zawierać
dokładnie jedną liczbę całkowitą, równą minimalnej liczbie
dni, jakie odpady muszą spędzić na terytorium państwa.
Przykład
Dla danych wejsciowych:
9 2 3 1 3 2 3 4 3 4 5 4 6 7 4 5 8 9 6 2 1 2poprawnym wynikiem jest: 4 |
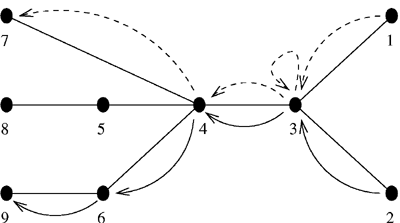 Strzałki przedstawiają ruch pociągów w kolejnych dniach dla jedej z optymalnych organizacji ruchu kolejowego - pętla oznacza, że danego dnia pociąg stał w mieście-węźle. |

Wersja do druku