Omówienie zadania Rozwiązanie pokojowe (I etap XXXIII OI, tura zdalna)

Treść zadania

W zadaniu rozważamy szachownicę \(n \times n\), gdzie \(n\leq 100\), na której – na podanych polach – stoi \(k\leq 2500\) ponumerowanych królów szachowych. Znamy także docelowe ustawienie królów, przy czym istotne jest, że na danym polu docelowym ma stać król o podanym numerze, a nie dowolny. Należy podać dowolny ciąg ruchów (długości \(\leq 5\cdot 10^6\)), po wykonaniu których króle znajdą się na polach docelowych. Jednak w żadnym momencie podczas wykonywania tych ruchów żadne dwa króle nie mogą się „bić”, czyli zajmować pól stykających się bokami lub rogami (przy czym ustawienia początkowe i docelowe z założenia spełniają ten warunek).

Podział na kwadraty

Gdy zastanawiamy się, ile maksymalnie królów można ustawić na szachownicy, naturalnym pomysłem jest rozstawienie ich co dwa pola, w równych odstępach, tworząc regularną kwadratową siatkę. Czy jednak jakieś nieregularne ustawienie nie okazałoby się lepsze? Otóż nie. Aby to zrozumieć — i ułatwić sobie analizę całego zadania — podzielimy szachownicę na kwadraty \(2 \times 2\), jak na rysunku poniżej. Jeśli rozmiar planszy jest nieparzysty, to kwadraty przy jej brzegach (te z prawej i na dole) będą częściowo wystawały poza obszar szachownicy.

Cztery pola w jednym kwadracie nawzajem do siebie przylegają, co oznacza, że w każdym kwadracie może znajdować się co najwyżej jeden król. Z drugiej strony, lewe górne pola wszystkich kwadratów (oznaczone kropkami na rysunku powyżej) nie przylegają do siebie. Jeśli więc króle stoją tylko na tych lewych górnych polach, nie będą sobie nawzajem przeszkadzać. W szczególności, każdy król może bez problemu przejść do sąsiedniego pustego kwadratu (w kierunkach dół, góra, prawo, lewo; nie na ukos), wykonując dwa ruchy w danym kierunku.

Zatem, w ramach przygotowania, na początku przemieśćmy wszystkich królów na lewe górne pola swoich kwadratów. Następnie wykonamy – opisaną w dalszej części tekstu – podprocedurę, która umieści każdego króla w jego docelowym kwadracie, a na końcu przesuniemy go na docelowe pole wewnątrz tego kwadratu. Wymagana jest tu minimalna ostrożność, aby podczas tego przesuwania króle nie przylegały tymczasowo do siebie. Wystarczy jednak, aby przy początkowym przesuwaniu kwadraty były przetwarzane od góry i od lewej; wtedy, gdy król idzie do lewego górnego rogu, to pola o jedno pole wyżej i po lewej są już na pewno zwolnione. Przy końcowym korygowaniu pozycji postępujemy odwrotnie: przetwarzamy kwadraty od dołu i od prawej, ponieważ tym razem króle w obrębie swoich kwadratów przesuwają się w prawo i/lub w dół (król może zostać przesunięty, ponieważ króle znajdujące się poniżej i po prawej są już na swoich docelowych pozycjach, które z założenia nie przylegają do docelowej pozycji naszego króla).

Sprowadziliśmy więc oryginalne zadanie do nieco innego: mamy teraz kwadraty; w każdym z nich jest co najwyżej jeden król, który może przejść do jednego z czterech sąsiednich kwadratów, pod warunkiem że kwadrat docelowy jest pusty (okazuje się, że to nie jedyne możliwości przemieszczania króli, o czym będzie mowa później). Przypomina to popularną łamigłówkę, w której należy ułożyć obrazek, przesuwając kwadraty na sąsiednie pola. W tej łamigłówce brakuje jednak dokładnie jednego elementu, podczas gdy u nas liczba królów jest dowolna.

Zapewniamy pusty róg

Rozważmy najpierw przypadek, gdy w każdym kwadracie stoi król. Wówczas żaden król nie może przejść do innego kwadratu, ponieważ ten jest już zajęty. Jeśli więc w ustawieniu docelowym któryś król ma znaleźć się w innym kwadracie niż w ustawieniu początkowym, odpowiadamy NIE. Natomiast jeśli kwadraty mają pozostać te same, nie musimy podejmować żadnych działań (jedynie skorygować położenia wewnątrz kwadratów, co już zostało zrobione poza omawianą teraz podprocedurą).

W dalszej części tekstu założymy, że przynajmniej jeden kwadrat jest pusty. Aby uniknąć rozważania dodatkowych przypadków, wygodnie byłoby, gdyby na koniec pusty kwadrat miał znaleźć się w konkretnym miejscu, najlepiej w rogu – powiedzmy w prawym dolnym rogu. Można to zapewnić wykonując pewne ruchy „w tył” z ustawienia docelowego. Powiedzmy, że (idąc w tył) przesuwamy wszystkich królów (w kolejności od góry i od lewej) maksymalnie w górę, a następnie maksymalnie w lewo. Dzięki temu w nowym ustawieniu docelowym (z którego opisanymi ruchami przejdziemy do „prawdziwego” ustawienia docelowego), w każdym wierszu najpierw będą kwadraty zajęte, a potem wolne, jak również w każdej kolumnie będą najpierw kwadraty zajęte, a potem wolne.

Typowy kwadrat

Będziemy teraz układać naszą układankę od góry, a każdy kolejny wiersz – od lewej do prawej. Typowa sytuacja wygląda więc tak, że chcemy ułożyć pewien kwadrat X, a wiersze powyżej X oraz kwadraty na lewo od X są już ułożone.

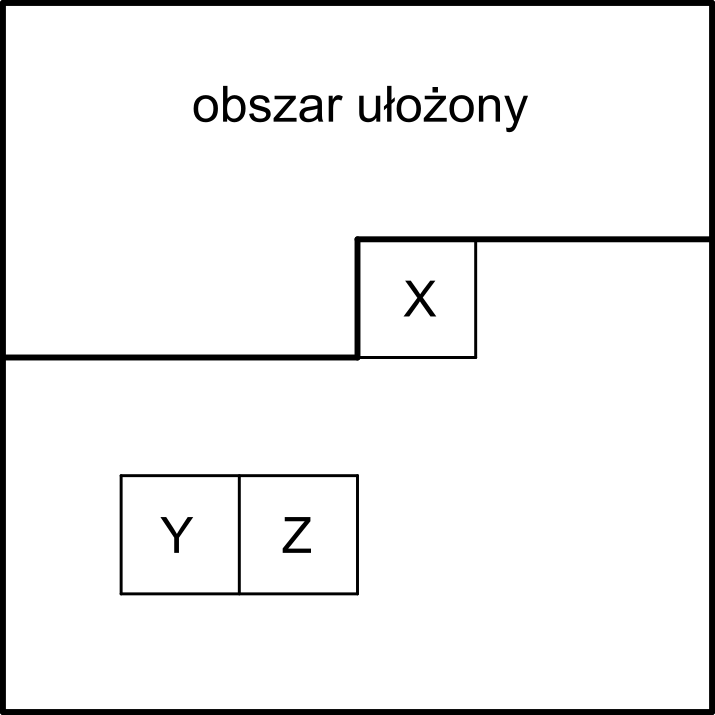
Załóżmy najpierw, że kwadrat X nie należy do ostatnich dwóch kolumn ani do ostatnich dwóch wierszy (te przypadki trzeba rozważyć osobno). Jeśli docelowo kwadrat X ma być pusty, wystarczy sprowadzić tam dowolne puste pole: przesuwamy je najpierw w prawo lub w lewo do odpowiedniej kolumny, a następnie w górę do X (przesuwanie pustego pola do sąsiedniego kwadratu to tak naprawdę przesuwanie króla z tego docelowego kwadratu w przeciwnym kierunku; jeśli króla tam nie ma, to nic nie musimy robić).

Ciekawsza jest sytuacja, w której na X ma znaleźć się król, stojący obecnie na pewnym kwadracie Y. Będziemy również przesuwać go najpierw w poziomie, a potem w pionie (nie odwrotnie, aby nie zburzyć już ułożonych kwadratów na lewo od X). Przesunięcie króla na sąsiedni kwadrat Z jest możliwe jedynie wtedy, gdy Z jest pusty. Musimy więc najpierw sprowadzić puste pole na kwadrat Z, omijając kwadrat Y (nie chcemy cofnąć króla z Y w przeciwnym kierunku). Jak to zrobić technicznie? Można na przykład przesuwać puste pole w stronę kwadratu Z, jednak gdybyśmy mieli przejść przez kwadrat Y, to go okrążamy. Należy jednak zwrócić uwagę, aby okrążyć kwadrat Y z odpowiedniej strony, ponieważ może on przylegać do któregoś z brzegów albo do granicy już ułożonego obszaru. Wybieramy więc taki kierunek okrążania, który jest dostępny. Zauważmy też, że może wystąpić potrzeba przesuwania pustego pola w dół, co należy zrobić przed przesuwaniem go w lewo (odwrotnie byłoby źle, jeśli zaczynalibyśmy z wiersza zawierającego X). Gdy kwadrat Z będzie już pusty, możemy przesunąć króla z kwadratu Y na Z i całą procedurę powtórzyć, aż król dotrze na pole X. Ważne jest, aby przy kolejnych ruchach króla korzystać z „tego samego” pustego pola, a nie sprowadzać nowego pustego pola za każdym razem z daleka – w przeciwnym razie łączna liczba ruchów byłaby za duża.

Ostatnie kolumny

Omówmy teraz układanie ostatnich dwóch kwadratów w kolumnie. Oznaczmy te dwa kwadraty oraz kwadraty w dwóch wierszach pod nimi kolejno literami A, B, C, D, E i F, jak na rysunku poniżej.

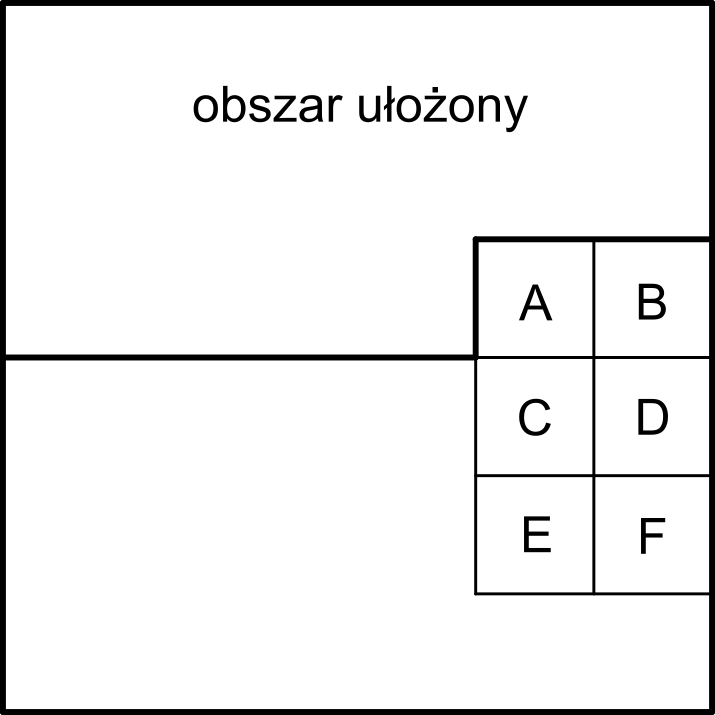
Zacznijmy od zauważenia, że jeśli kwadrat B ma docelowo pozostać pusty, nie musimy niczego zmieniać: sprowadzanie króla (lub pustego pola) na kwadrat A metodą opisaną wcześniej działa bez zarzutu, a sprowadzenie pustego pola na kwadrat B również nie sprawia kłopotów.

Możemy więc przyjąć, że na obu kwadratach A i B ma ostatecznie stanąć król. W takiej sytuacji pojawia się jednak pewien problem: jak wprowadzić króla na kwadrat B, nie wysuwając jednocześnie króla z kwadratu A. Dlatego sprowadźmy najpierw króla \(b\), który ma ostatecznie znaleźć się na kwadracie B, na kwadrat A.

Następnie postępujemy w ten sposób (o ile to możliwe, o czym za chwilę): króla \(a\), przeznaczonego na kwadrat A, sprowadzamy najpierw na kwadrat C, po czym wprowadzamy puste pole na kwadrat B, omijając kwadrat C. Gdy już to zrobimy, możemy po prostu przesunąć króla \(b\) z A na jego docelowy kwadrat B, a następnie przesunąć króla \(a\) z C na jego docelowy kwadrat A.

Powyższa procedura jednak nie zadziała, jeśli król \(a\), którego chcemy umieścić w kwadracie C, jest „uwięziony” na kwadracie B. Nie powiedzie się również wtedy, gdy król ten znajduje się na kwadracie D, ale puste pole potrzebne do manewrowania leży na kwadracie B. W takich przypadkach, zanim zastosujemy naszą procedurę, postępujemy następująco: Najpierw sprowadzamy poste pole na kwadrat D (w drugim z opisanych przypadków przychodzi ono z kwadratu B, a król \(a\) z D wraca na B; od tego momentu oba warianty są już identyczne). Następnie przesuwamy króla \(a\) z B na D, a króla \(b\) z A na B. Kolejnym krokiem jest sprowadzenie pustego pola na kwadrat F (omijając kwadrat D), po czym przenosimy króla \(a\) z D na F. Na koniec przesuwamy króla \(b\) z B na A, uprzednio sprowadzając puste pole z D przez C na A. W ten sposób uzyskujemy sytuację, w której opisana wcześniej procedura może zostać bezproblemowo zastosowana – uda się przemieścić króla \(a\) z E na C, a następnie wsunąć królów z A i C odpowiednio na B i A.

Ostatnie wiersze

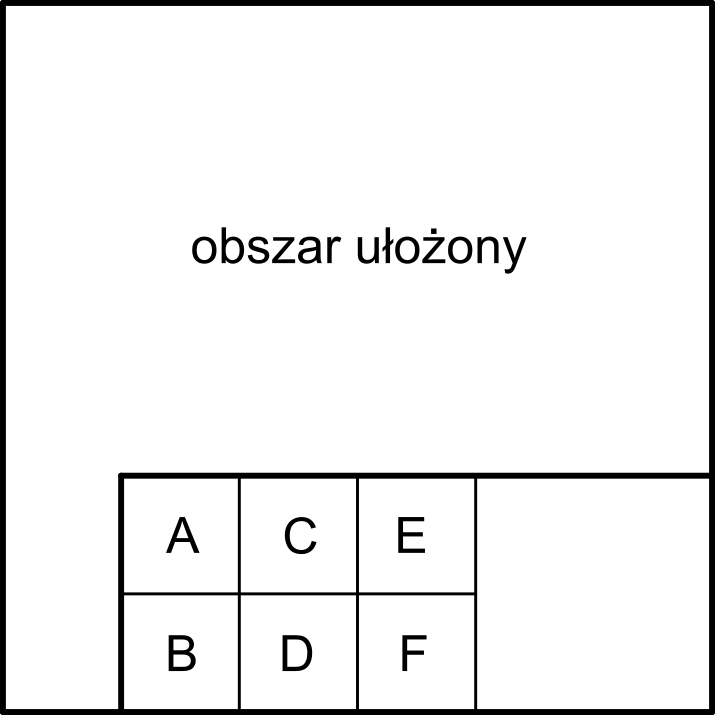
Ostatnie dwa wiersze układamy równocześnie, przesuwając się od lewej do prawej. Procedura jest całkowicie symetryczna względem tej, którą stosowaliśmy do ułożenia ostatnich dwóch pól w wierszu. Co prawda tym razem wiersze znajdujące się wyżej są już ułożone (a więc nie można ich naruszać), podczas gdy wcześniej kolumny po lewej nie były jeszcze całkowicie uporządkowane, jednak ta różnica nie wpływa na przebieg naszej procedury. Układ kwadratów A, B, C, D, E i F w tej nowej sytuacji przedstawia rysunek poniżej.

Ostatnie cztery kwadraty

Pozostaje nam ułożyć ostatni fragment planszy o wymiarach \(2\times 2\) kwadraty. Oznaczmy te kwadraty kolejno literami A, B, C i D.

Ogólną metodą sprowadzamy najpierw właściwego króla na kwadrat A. Jeśli oba kwadraty w ostatniej kolumnie mają pozostać puste, wówczas króla stojącego ewentualnie na B przesuwamy na D, a następnie króla znajdującego się ewentualnie na D przenosimy na C. Analogicznie, jeśli oba kwadraty w ostatnim wierszu mają pozostać puste, przesuwamy króla z C (jeśli tam jest) na D, a następnie króla z D (jeśli tam jest) na B.

Pozostaje nam przypadek, w którym jedynym pustym kwadratem ma być D. Sprowadźmy więc puste pole na D. Jeśli króle na kwadratach B i C stoją już prawidłowo, to wszystko jest gotowe. Jeśli jednak tak nie jest, musimy je zamienić miejscami. Czy jest to możliwe?

Otóż, gdy \(n\) jest parzyste, okazuje się, że tak! Musimy jednak przyjrzeć się poszczególnym polom, a nie całym kwadratom. Mianowicie, króla z kwadratu B możemy przesunąć w sam róg planszy. Między nim a królem stojącym na kwadracie A jest wystarczająco dużo miejsca, aby król z kwadratu C mógł „przecisnąć się” na kwadrat B. Na koniec sprowadzamy króla z rogu na właściwe miejsce w kwadracie C.

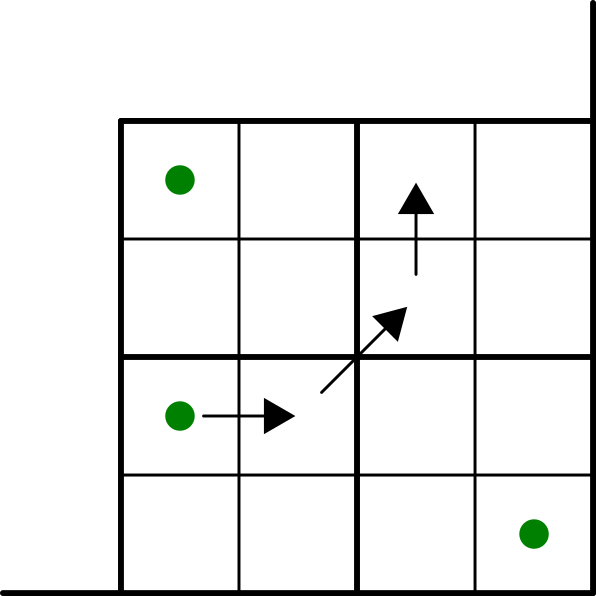
Zobaczmy, że gdy \(n\) jest nieparzyste, takie „przeciskanie się” (gdziekolwiek na planszy) między kwadratami położonymi względem siebie na ukos nie jest możliwe. Przeciskanie interesuje nas wyłącznie wtedy, gdy na planszy jest tylko jeden wolny kwadrat – musi to być dokładnie ten kwadrat, na który nasz król chce się przedostać. Aby jednak przeciskanie było możliwe, król w jednym z dwóch dolnych kwadratów musiałby stać w dolnym wierszu. Wówczas we wszystkich kwadratach położonych niżej króle także musiałyby zajmować dolne wiersze swoich kwadratów. Jest to jednak niemożliwe, ponieważ w najniższym kwadracie dolny wiersz wypada już poza planszę.

Zatem dla nieparzystego \(n\) możliwe są jedynie ruchy między kwadratami sąsiadującymi bokami. Jest powszechnie znaną własnością, że jeśli tylko jeden kwadrat jest pusty, nie da się zamienić miejscami wyłącznie królów z dwóch sąsiednich kwadratów, pozostawiając niezmienione ustawienie pozostałych. Dowód tego faktu pominiemy (opiera się on na analizie parzystości odpowiedniej permutacji). Wnioskujemy natomiast z tej własności, że jeśli króle na kwadratach B i C są zamienione, nie da się tego naprawić – musimy odpowiedzieć NIE.

Liczba ruchów

Można zauważyć, że rozwiązanie sprowadza się do podążania każdym z \(k\) królów na jego docelową pozycję, znajdującą się w odległości co najwyżej \(2n\) pól od jego aktualnej pozycji. W międzyczasie inne króle muszą ustępować drogi, jednak na jeden ruch rozważanego króla tych dodatkowych ruchów innymi królami jest kilka (stała liczba). Do tego dochodzi przesunięcie pustego pola w pobliże króla na początku jego przemieszczania, a także korygowanie pozycji królów w końcowej fazie – w obu przypadkach nie więcej niż \(2n\) ruchów. Łączna liczba ruchów jest więc rzędu \(O(k\cdot n)\). Zgrubne oszacowanie liczby ruchów w przedstawionej metodzie daje ograniczenie poniżej \(2.2\cdot 10^6\) (dokładnych obliczeń nie będziemy tutaj przytaczać).

Szczegóły techniczne

W powyższym opisie jedynymi „nielokalnymi” operacjami są wyszukiwanie króla o zadanym numerze oraz znajdowanie wolnego kwadratu. Operacje te wykonujemy jedynie \(O(k)\) razy, dlatego naiwna implementacja w czasie \(O(n^2\)) (przeglądanie całej planszy) jest w zupełności wystarczająca.

Generowanych ruchów nie wypisujemy od razu, lecz zapisujemy je w odpowiedniej tablicy. Wypiszemy je dopiero na końcu, gdy będzie już znana ich całkowita liczba.

Widzimy zatem, że zadanie nie jest wcale wymagające algorytmicznie; należy jedynie uważać przy implementacji dość skomplikowanej metody przemieszczania królów. Pomocne jest zdefiniowanie odpowiednich procedur, na przykład: procedury doprowadzającej puste pole na kwadrat Z, omijając kwadrat Y, czy procedury przesuwającej króla numer \(i\) na pole X. Przydatne jest także operowanie na całych kwadratach zamiast na pojedynczych polach, tak jak zostało to pokazane w powyższym opisie.

Niezbędne wydaje się również dokładne przetestowanie programu. Dość prosto można napisać weryfikator, który przesymuluje wygenerowane ruchy i sprawdzi, czy są one poprawne oraz czy faktycznie prowadzą do konfiguracji docelowej. Następnie program można uruchomić na pewnej liczbie losowych plansz różnego rodzaju – z wszystkimi kwadratami zajętymi, z jednym pustym kwadratem oraz z większą liczbą pustych kwadratów.